| |
| Inicio |
| Objectivos |
| História |
| Geometria |
| Analise Estrutural Simplificada |
| Conclusão |
|
Metodologias simplificadas para análise estrutural. Aplicação ao caso de estudo do troço do Aqueduto dos Pegões localizado na Quinta Nova da Raposa Análise simplificada com base no traçado da linha de pressões Com o objectivo de avaliar o factor de segurança nos arcos do Aqueduto dos Pegões, foi utilizado um programa de cálculo automático denominado RING que permite avaliar a carga máxima, que corresponde à formação de um mecanismo de colapso no arco, recorrendo à identificação de linha de pressão no arco. Assim, foram consideradas características da geometria do Aqueduto, aferido com base na técnica de fotogrametria descrita anteriormente. Os parâmetros dos materiais (pedra, enchimento e interfaces entre elementos) foram definidos através dos valores identificados em estudo precedentes. Considerou-se que os materiais possuem resistência à tracção nula e resistência à compressão ilimitada. Tab.: Parametros dos materiais. Para simular as situações mais gravosas, cujas acções serviram de base a esta análise simplificada, foram tidas em conta: o peso próprio da construção, uma sobrecarga uniformemente distribuída e uma carga pontual localizada em pontos seleccionados. Os valores referentes ao peso próprio dos materiais foram estimados com base nos resultados já referidos anteriormente. A influência das cargas exteriores baseou-se na aplicação de cargas unitárias distribuídas numa extensão correspondente a metade do vão e centradas a meio vão e a um terço do vão dos arcos (ver figura relativa à acção distribuída). A influência da carga pontual, no mesmo conjunto de arcos, foi estudada através da aplicação de forças concentradas unitárias em três pontos distintos: a um quarto do vão a meio vão e sobre o pilar (ver figura relativa à acção pontual). No contexto das metodologias utilizadas, no programa Ring, as cargas exteriores (distribuídas e pontuais) são agravadas por um coeficiente monotonicamente crescente, no sentido de avaliar o factor multiplicativo, que agrava essas acções, determinando-se assim o factor de segurança relativo a essas solicitações. Este factor de segurança representa um coeficiente (majoração) que, multiplicado pelas cargas actuantes na estrutura, conduz a uma situação de colapso. Resultados
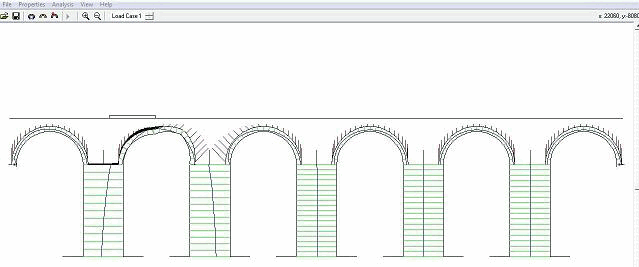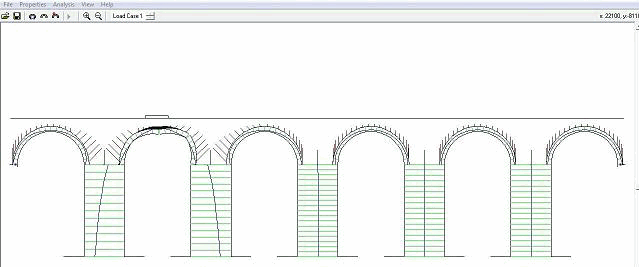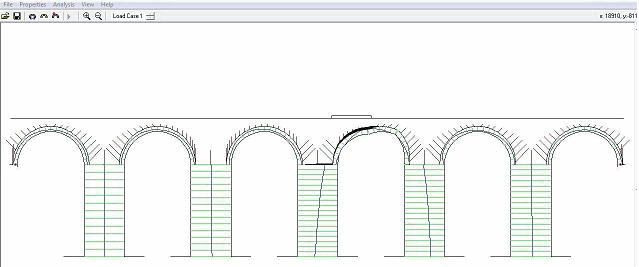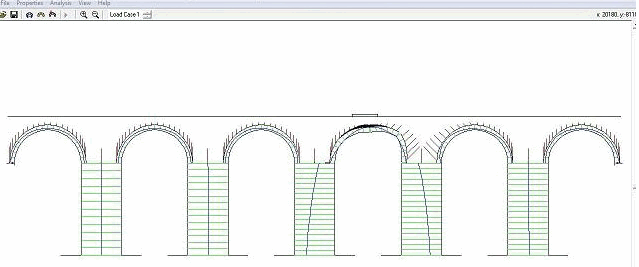
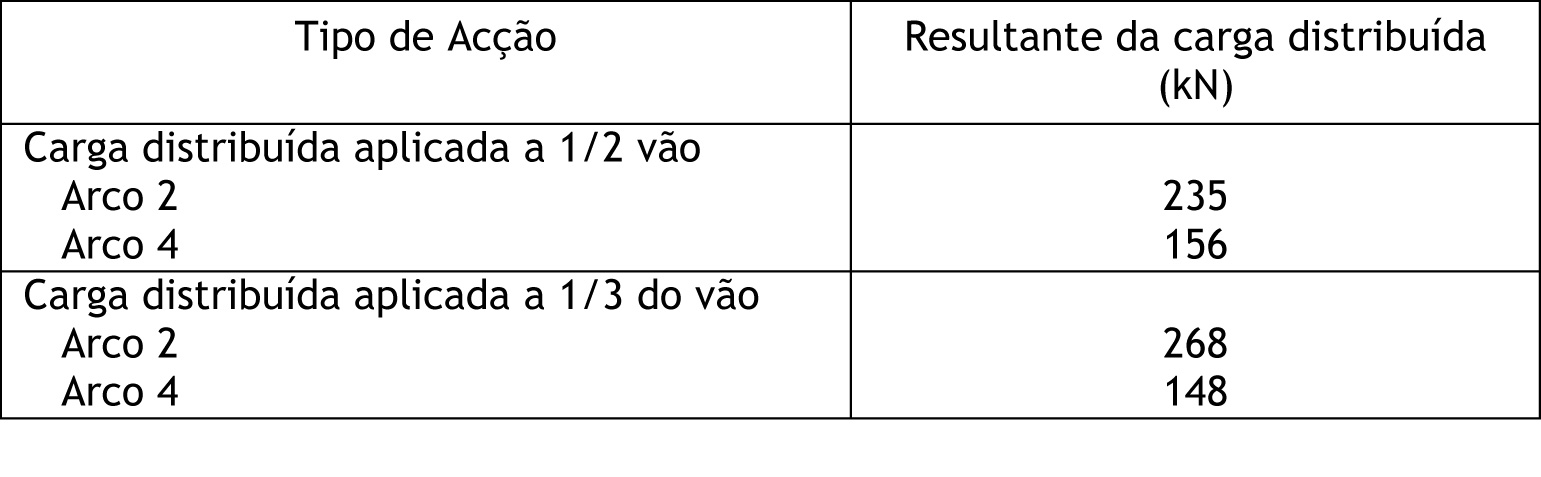
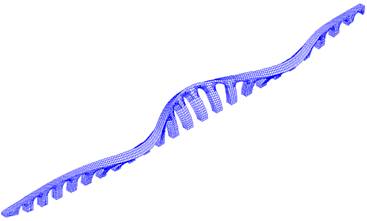
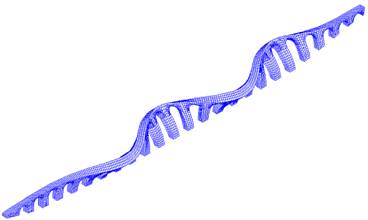
Fig.: Mecanismo de colapso para a carga distribuída. Tab.: Resultante da carga distribuída correspondente aos mecanismos de colapso nos arcos 2 e 4.
Fig.: Mecanismo de colapso para a carga concentrada. Tab.: Carga concentrada correspondente aos mecanismos de colapso nos arcos 2 e 3.
Como se pode constatar a situação mais desfavorável ocorre no arco 2 quando é aplicada uma carga pontual a meio-vão. Atendendo ao valor obtido, 91 KN, é possível avaliar o factor de segurança da estrutura para um determinado nível de carga esperado. Não existindo regulamentação específica para este tipo de estruturas, considera-se a título de exemplo uma carga pontual de 10 KN aplicada a meio-vão no arco 2. Para esta solicitação obtém-se um factor de segurança de 9.1. Trata-se, de facto de um valor bastante elevado que atesta a robustez da estrutura. No entanto é necessário ter em consideração que na metodologia usada se considerou que a resistência à compressão do material é infinita, pelo que aquele factor de segurança será naturalmente inferior se o limite de resistência à compressão dos materiais for considerado na análise. Quando a carga é aplicada a 1/3 ou 1/4 do vão os esforços repartem-se por uma área maior do arco através do enchimento. Por esta razão, se encontram para a situação da aplicada a meio vão as situações mais desfavoráveis, pois nesta zona existe uma reduzida espessura de enchimento na parte superior do arco. Análise simplificada recorrendo ao Método dos Elementos Finitos Com o objectivo de avaliar o nível de tensões máximas actuantes no troço em estudo do Aqueduto dos Pegões, localizado da Quinta Nova da Raposa, e compará-las com as tensões máximas admissíveis dos materiais usados na construção procedeu-se a uma análise elástica linear (simplificada) com base no Método dos Elementos Finitos recorrendo ao programa Cast3m. A estratégia usada nesta análise consistiu em descrever a geometria, aferida anteriormente com auxílio da fotogrametria, através de elementos finitos tridimensionais de modo a representar o contínuo usando um único tipo de material elástico, isotrópico e homogéneo em toda a estrutura. A caracterização das propriedades elásticas dos materiais baseou-se em valores encontrados na bibliografia tendo em conta o tipo de material existente no local e outros valores usados em estudos precedentes que recorreram a metodologias de análise semelhantes. Geometria As dimensões dos pilares e dos arcos foram aferidas com auxílio da técnica da fotogrametria, que permitiu definir o alçado apresentado anteriormente e no qual se teve a preocupação de incluir alguns detalhes da estereotomia da pedra mas que nesta fase não foram incluídos na descrição da geometria por se considerar o material homogéneo. Assim, e tendo por base o referido alçado, redesenhou-se o alçado simplificado do troço em estudo do aqueduto que pode ser observado na figura seguinte. . Fig: Geometria simplificada considerada na análise linear elástica. Com a introdução de uma espessura constante de 1,45 metros ao longo de toda a estrutura e a utilização de elementos volumétricos de 8 e 6 nós, definiu-se a malha que pode ser observada na figura seguinte em alçado, planta e em perspectiva.
Fig.: Alçado da malha de elementos finitos
Fig.: Planta da malha de elementos finitos
Fig.: Prestectiva da malha de elementos finitos Parâmetros dos materiais Os materiais que compõem a estrutura são a alvenaria (blocos e juntas) e enchimento que foram representados num único material. Deste modo os parâmetros do material resultam de uma homogeneização dos parâmetros de cada constituinte formado por blocos, interfaces e enchimento. No contexto da simulação numérica de estruturas antigas de alvenaria de pedra a definição dos parâmetros dos materiais é uma das tarefas mais complexas de realizar. A estimativa das frequências naturais por via numérica e a sua comparação com idênticos parâmetros por via experimental constitui uma ferramenta preciosa para calibrar os modelos numéricos. No caso da análise que se apresenta e dado que não foi possível aferir no local os parâmetros da estrutura, avaliou-se a sensibilidade das características dinâmicas da estrutura em termos dos modos de vibração e frequências naturais para diferentes valores do módulo de elasticidade homogéneo. Neste contexto, importa sublinhar que os resultados que se apresentam nos parágrafos seguintes têm cariz, essencialmente, qualitativo pelo que se deve atender aos pressupostos tidos em conta na análise. Assim, foram considerados para o módulo de elasticidade da estrutura homogeneizada, E, os valores de 4 GPa e 2.82 GPa definidos com base na bibliografia para estruturas de alvenaria de pedra aparelhada e um valor do coeficiente de Poisson de 0.2 que pode ser considerado um valor corrente para este tipo de estruturas. Para o Peso específico, considerou-se 25.17 kN/m3 que resultou de uma ponderação entre as partes constituídas por paramentos de pedra e de enchimento. Condições fronteira Foram impostos bloqueamentos dos deslocamentos (dx, dy, dz) dos nós da malha da base e dos paramentos laterais extremos do troço considerado. Na figura seguinte ilustram-se (a vermelho) os nos nós da malha (em alçado) nos quais foram introduzidos bloqueamentos dos deslocamentos dx, dy e dz.
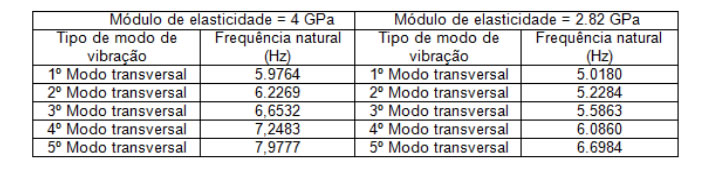
Fig.: Nós da base da malha de elementos finitos para definição das condições de apoio. Modos de vibração Com base no modelo definido de acordo com os critérios referidos nos parágrafos anteriores determinaram-se os cinco primeiros modos de vibração e frequências naturais da estrutura que se representam em alçado, planta e perspectiva nas figuras seguintes juntamente com o correspondente valor da frequência na legenda das figuras para o caso de um material com módulo de elasticidade de 4 MPa. No quadro resumem-se os valores das frequências e tipos de modos de vibração correspondentes para o caso referido anteriormente e também para o caso em que se considerou um valor do módulo de elasticidade de 2.82 MPa. Tab.: Frequências e modos de vibração.
Fig.: 1º Modo de Vibração
Fig.: 2º Modo de Vibração
Fig.: 3º Modo de Vibração
Fig.: 4º Modo de Vibração
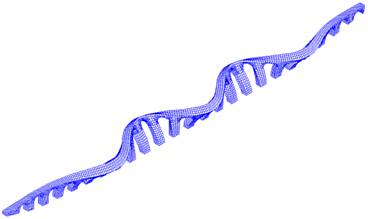
Fig.: 5º Modo de Vibração Atendendo aos resultados obtidos para os dois valores do módulo de elasticidade considerados verifica-se não existirem diferenças significativas na ordem e forma dos modos de vibração da estrutura. Em relação aos valores das frequências naturais verifica-se que uma redução de cerca de 30% do módulo de elasticidade reduz em 16% o valor da frequência fundamental. Neste contexto, optou-se por apresentar apenas os resultados referentes ao caso em que se considerou o valor de 4 GPa para o módulo de elasticidade homogéneo. Carregamento Nesta análise foram consideradas as acções do peso próprio da estrutura (cuja resultante vertical corresponde a 10291 KN) e uma carga distribuída de 5 KN/m2 aplicada em toda a superfície do aqueduto (nos elementos da superfície da malha marcados a vermelho no alçado e uma carga de faca de 3.4 kN/m aplicada a meio vão do décimo primeiro arco a contar da esquerda (nos nós representados a vermelho, nas figuras seguintes. . Fig.: Nós da malha de elementos finitos para aplicação da carga distribuída. Resultados Deformada Considerando as acções do peso próprio, das cargas distribuída e concentrada, obteve-se o valor máximo do deslocamento vertical de 0,22 mm e a deformada que se apresenta na Figura seguinte para a análise em que foi considerado um valor do módulo de elasticidade de 4 GPa. Quando é usado o valor de 2.82 GPa para o módulo de elasticidade obtém-se um deslocamento máximo de 0.32 mm.
Fig.: Deformada para a acção do peso próprio.
Tensões Principais Em relação às tensões principais máximas, para o conjunto das solicitações referidas anteriormente, obtiveram-se as distribuições das tensões principais máximas mostradas nas figuras em baixo, cujo valor máximo de tracção registado foi de 0.089 MPa, e o traçado dos vectores que representam a orientação das tensões principais são também ilustrados.
Fig.: Distribuíção das tensões principais máximas
Fig.: Direcção das tensões principais máximas A distribuição das tensões principais mínimas e respectiva orientação das tensões apresentam-se nas Figuras seguintes. Para o conjunto das solicitações referidas anteriormente o valor máximo de compressão registado foi de -0.24 MPa.
Fig.: Distribuíção das tensões principais mínimas
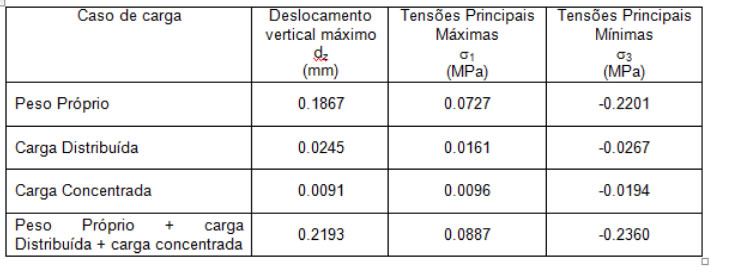
Fig.: Direcção das tensões principais mínimas No quadro seguinte resumem-se os valores máximos do deslocamento vertical e das tensões principais obtidos na análise para o caso de carga referido anteriormente apresentando-se também as parcelas correspondentes a cada solicitação independente. Tab.: Resultados da análise linear elastica.
Como resultado da análise simplificada atendendo aos valores obtidos para as tensões principais máximas e mínimas verifica-se serem muito inferiores aos valores das tensões resistentes admissíveis dos materiais. Para o caso de estruturas de alvenaria de pedra aparelhada o valor da resistência à compressão do material compósito (blocos, argamassa e interfaces), será próximo de 4 MPa. Para os blocos de pedra aquele limite situa-se na ordem dos 69 MPa.
|